25頭の馬の中から、速い順に3頭の馬を見分ける前問では、選ぶという観点から解くのではなく、ダメな馬を取り除いていくという発想、それを糸口にして解き進めることにより、短時間にすっきりした形での解答を得ることができました。

　面接試験に出されるような問題には、このように真正面から見るのではなく、裏から見る発想、それが功を奏することも頻繁にありますので、このような見方を常に身につけておかれることをお薦めします。

　さて、今号の設問はどうでしょうか。やはり裏から見る発想が手がかりになります。

　「153人もの人数がいれば、中には同じ回数の握手をした人は、一組くらいいるのではないだろうか、しかし自信を持って必ずいると言いきれるかと問われれば、その確認の仕方までも含めて、答に窮してしまう。」というのが、ごく一般的な反応かもしれません。

　握手の問題は手を変え品を変え、いろんな形でよく出題されますが、これはアメリカの大手コンサルタント会社における面接試験の問題です。
　皆さんの中には、初めてこの種の問題を見たという方もあれば、過去、これに類似した問題に触れたことがある方もおられるものと思います。

　例えば、類似の問題として
「40人のクラスの生徒の中に、友達の人数が全く同じである人が必ずいます。なぜか？　もちろんここでＡさんがＢさんの友達であれば、ＢさんもＡさんの友達であるとする。」
といったものがあります。

　しかしこの友達の問題を初めて見る方たちの中には、「それはおかしい。もしも40人の新入生に対する最初のクラス編成の時を考えれば、最初から友達なんていないのが普通で、そもそも友達の人数を云々する問題としては成り立たないのではないか」と、疑問に思われる人もいるかもしれません。
　このような疑問は当然のこととして、以下、読み進むに従って設問の「なぜか」がわかってきます。

また次の問題、
「人口が少なくとも20万人の都市には、頭髪の本数がまったく同じである人の組が何組か存在する。なぜか。」

というのも、一見、風変わりで分野の違う問題のように見えますが、これも類似の同じ部類に属する問題です。
この問題についてもあとで解説をしますが、本設問を解いていくことにより、「なぜそうなのか」が自ずとわかってきます。

　では、本問の解説に入ります。
　まずこの153人という人数ですが、先にも述べたようにこれだけの人数がいれば、中には同じ回数の握手をした人はいるのではないだろうかと、単に回答者にそう思わせるために用意された人数なのか、

あるいは153という数そのものに意味があるのか、152や154ではダメなのか、またキリのいい150や160あるいは140では意味がないのかなどと、さらに疑問を重ねていった方もおられたかもしれません。

　そこでいろんな問題の糸口、手がかり、突破口を探すためにまとめた当連載その73にある対処法を見てみますと、その中で、この設問111に適用できそうなのは「数量が多い問題は小さな数字や量で単純化、シンプル化してやってみる」か、あるいは「長々とした文章の問題などは、隠れているもの、裏にあるものを考えてみる」があります。

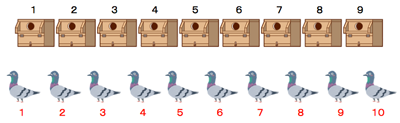
　実は、この種の問題で見られる世の中の解法は、すべて「鳩ノ巣」原理で解いています。10羽の鳩を9個の巣箱に割り振ろうとすると、どうしても２羽以上が入る巣箱が出てくる、というしごく単純な原理です。
　この原理を使うための糸口が、まさしくここにある「裏にあるものを考えてみる」で、前問110の「速い馬選び」の問題もそうだったように、問題を真正面から見るのではなく、視点を変えて裏から見ることにより、すっきりと解けてくるのです。

では、この問題を裏から見るとはどういうことか。
それは出題の「この会場で、同じ数の握手をした人が最低2人はいる」を裏から見て、「この会場で、同じ数の握手をした人は1人もいない」の否定形である、というふうに考えるのです。そして、それを証明すればいいということです。

　そこで、「同じ数の握手をした人は1人もいない」、つまり「全員の握手の回数が違う」とすると、どうなるかを見るわけです。
　握手は自分自身ではしませんから、153人の場合、考えられる握手回数の全種類は0回から152回の153種類になり、ここで153人全員握手の回数が違うとすると、0回から152回の人が1人ずつ居ることになります。

　すると矛盾が出てくるのです。152回の人は全員と握手をしているのに、握手をしていない0回の人も、その中にいるという矛盾です。
　これを分かり易く説明するのが「鳩の巣」原理です。
　ここで当設問の全員がその握手回数が違うとして、握手の回数ごとの0から152までの153個のボックスを用意し、0回の人から1人ずつ順番にそれぞれのボックスに入っていってもらうのです。

　そして152番目のボックスに入る人の番になったとき、どうなるか。
すでに0回の人がいますから、152人全員と握手した人はいなく、152番目の人は自分の握手した回数に従って、すでに他の人が入っている0～151番のボックスのどれかに入ることになり、どこかのボックスには、必ず2人いることになるのです。
　つまり握手した人数が同じ人は、確実に２人はいることになるということです。

　では、この「鳩の巣」原理を使わない場合はどうか。
それは、前述対処法の「数量が多い問題は小さな数字や量で単純化、シンプル化してやってみる」です。

　握手の問題ですから、1人ではなく2人の場合を見てみます。

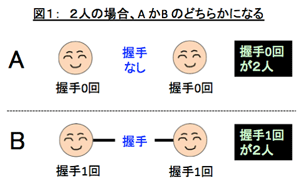
起こり得る握手の回数は図１のように0回か、1回ですが、ここで握手という特殊な背景があるということに気づくことになり、この気づきが正解へと導くわけです。

　つまり握手というのは、常にペアで成立するという点です。握手が0回でも1回でも、ペアですからいずれの場合も必ず2人いるということです。
　ということは、これが握手の基本形になりますから、3人（図２と図３）、4人と人が増えていっても、どのペア2人にも必ずこの形が適用されることになり、したがって握手の回数が同じになる人は、少なくとも2人は居るということになるのです。

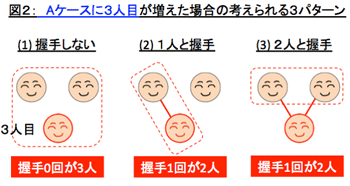
　ここに至ってこのような問題では、特定の人数とはまったく無関係だということがわかると思います。10人でも60人でも200人でも、同じなのです。
　したがって、前述の友達の問題もこれでわかると思います。
また新入生の最初のクラス編成時で疑問に思った方も、友達がいない、つまり友達が0人の場合を忘れたことに起因するもので、この0人の場合を入れれば、友達の人数が全く同じである人が必ずいることになります。

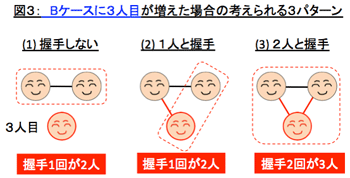
　　では、前述の「頭髪の本数がまったく同じ人」の問題はどうか。
この問題は、あらかじめ人間の頭髪の本数がどれくらいかを知らないと解けないのでは、と思われるかもしれません。しかしここで前述の鳩の巣の原理がちらっとでも脳裏をよぎっていさえすれば解けたも同然だということです。

　つまり問題の中に出ている人口の20万人とこの原理を結びつけて考えれば、頭髪の一番多い人でも20万本以下ということを前提にした問題ではないかと予見でき、この原理を使えるからです。
　そして次に、本連載愛読者になじみの深いフェルミ推定でもって、一般人の頭髪数を考えてみればいいわけです。

　対象として自分の頭髪によるフェルミ推定はどうでしょうか。
たとえば1本の頭髪とその周りの頭皮が占める面積を0.5mm²とすると、1cm²=100 mm²当たりでは100/0.5=200本。頭皮の表面積は10cm四方が6個くらいあるとして600cm²。したがって頭髪の本数は200ｘ600=120,000本ほどと概算値が出ます。

　したがって、どんなに頭髪の密度が濃い人でも、あるいは頭皮の広い人でも、この7割増しともなる20万本の人は、もはやいないと考えられるのです。

　実際、頭髪数に関する資料を調べてみますと、黒髪の場合はせいぜい10万本、ブロンドの場合は15万本ほどと出ています。
　そこで十分な余裕をみて199,999個のボックスを用意し、20万人都市の人を自分の頭髪数に従ってそこに入ってもらうとすると、鳩の巣原理からどれかのボックスには、必ず2人以上の人が入らざるを得なくなり、20万人都市では、頭髪数がまったく同じの人が少なくとも2人は居ることになります。

　さらにスキンヘッドの人ももちろんたくさんいると思いますが、大部分の人たちは、おそらく10万本から15万本のあたりに集中しているはずで、この本数近辺のボックスには、2人以上入る組が何組も出てくると予想されるわけです。

　余談になりますが、人間の髪の毛は母親の体内にいるときにはすでに生えていて、その段階で各人の髪の毛の本数は決まっており、以降それ以上増えることはないそうです。
　また大人の髪の寿命は、男性の場合2〜6年、女性の3〜7年で、その間に全ての髪がすっかり入れ替わるとのことです。

　この設問は鳩の巣原理を応用できるような頭脳の持ち主かどうか、また鳩の巣原理の応用をしないとしたら、出題者側を納得させることのできるような他の説明ができるかどうか、その論理思考過程などを見ようとしているものです。

　それでは設問111の解答です。

　では、次の問題の出題背景を考えながらやってみてください。これはヒューレット・パッカード社が新卒採用面接で出した試験問題です。