未知・未経験の世界での問題解決能力、そしてそこでの新たな創造力、いわゆる自ら考える頭脳が必要不可欠になってきている新たな時代に突入して、アメリカのIT企業やコンサルタント企業の多くが、面接試験でその能力を見るための問題を盛んに出題するようになり、さらに正解を問うのではなくその思考過程、いわゆる「考えるプロセス」を見る典型的な問題・フェルミ推定も含めて、このトレンドは日本企業にも押し寄せてきました。

　これに伴って、大学入試も変えていこうと、知識偏重で１点を争うテストから、知識の活用力や思考力、主体性を評価して面接やプレゼン能力を問い、学力を測る場合は選択式だけでなく、「記述式、論述式」にするとして、「思考力・判断力・表現力」を見るものに変えていこうとする中央教育審議会の意向が、2014年の年末に発表されました。

　その内容は本シリーズの「その105」と「その106」に掲載していますが、この度、2015年12月末、さらに具体的な形でその例題問題が文科省から発表されました。

　例えば国語の問題は多様な見方や考え方ができる題材になっていて、その思考過程を見るものとして、図や文章を読み解く次のような例題が示され、自分の考えをまとめる力が求められるようになっています。

　その1つの例題とは、図のような3つのグラフを示し、
「交通事故の統計資料を見て､死者数が他より早く減少傾向になっていることについて高校生が話し合いました｡

　その解答例として
「救急車の出動回数については交通事故の発生件数や負傷者とほぼ同様に上昇傾向で推移しているのに対し､救命率については死者数の推移とは逆に上昇傾向で推移していること」

　と出ていますが、従来のマーク式や選択式から記述式へと大きく変わり、自ら考える力・その考えるプロセス・思考過程がわかるような問題になっています。

　いいよいよ日本でも時代の要請に応じて、このように大学入試も変わろうとしていますが、実は偶然か、あるいはこのことを意識してかわかりませんが、日本の小学校入試に格好の例がすでにありましたので、この機会にご紹介しておきたいと思います。
　その問題とは図のような絵を示し、「この中で仲間はずれはどれでしょう？」という問題です。

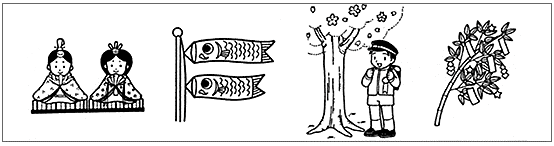
　当連載で、ビル・ゲイツの面接試験問題などにチャレンジされている皆さんからしてみれば、何で今さら幼稚園児を対象にした問題を、とお叱りを受けるかもしれませんが、まずはやってみてください。

　ここでしばし考えていただくために、なぜ格好の例なのかその理由や解答を、この巻末にまわしましたので、後ほどご覧ください。

　それでは、今号の設問に入ります。
 

　どうでしょうか。設問を見た瞬間、それだけで気後れしそうになる方も多かったかもしれません。
　というのも、水の量が関係するはずの数値として、プールの大きさに関する記述が一切ないことや、最初の水位の数値がないこと、また示されている分数の値が際限なく小さくなっていくことなどなど。

　さらにその上、最も悩ましく思うのは、1/3（=0.3333･･･）や1/6（=0.1666･･･）、あるいは1/7（=0.1428･･･）や1/9（=0.1111･･･）など、出てくるはずのほんの数個の分数を考えただけでも、その値は少数点以下が無限に続くような値で、はたして整数としての日数を表すことができるのか、といった疑念です。

　つまりこの設問は、数学の計算問題らしいことはわかりますが、プールの大きさがわからない、最初の水の高さもわからない、出てくる分数の中にも無限に続く少数点の数値がたくさんあるなどで、どうやって計算していけばいいのか。
　そんな中で、さらに、プールの形を直方体と言っている但し書きの意味は何なのか、といったことなどです。

　そこでこれまで度々参照したように、その手がかりや糸口、あるいはその突破口を見出すため、典型的な問題分野の対処法を列記した本シリーズの「その73」を振り返って見ると、その中にぴったりと当てはまりそうなものがあります。
　それは、「複雑に見える問題、数量が多い問題、読んだだけで気後れしてしまう問題、思考が発散してしまいそうな問題、長々とした文章の問題などは、目くらましの出題意図が前面に出ていることが多いので、まずは小さな数字や量で単純化、シンプル化してやってみる」です。

　さらに、わからないことがたくさん入っているこの問題が、れっきとした試験問題として出題されているということ、それはとりもなおさず、そこに示されている数値だけで、しっかりと解けますよ、という重要なポイントを示唆しているということです。
　たとえば最初に具体的な高さの数値が示されていないということ、それは逆に言えば、最初の高さはどんな数値でもいい、ということを意味していると考えられます。

　そこで高さを任意の数値にして、まずは「小さな数字」からやってみることにします。
　最初にオーナーがはった水の高さを仮に1cmとしますと、業者が1日目に、その1/2の高さの水の量を加えますから、結果
　1+(1x1/2)=1+1/2=3/2=1.5cm･･･(1)
となります。

　では2日目。今度は1日目の高さの1/3が追加されます。ここで1/3=0.3333･･･と少数点のことが頭にあると前に進めなくなってしまうのですが、分数のままで計算すると
　1.5+(1.5x1/3)=4.5/3+1.5/3=6/3=2cm･･･(2)
と、うまい具合に割り切れます。

ということは、この先に進んで1/6のときや1/7、1/9のときも、うまく割り切れるのではないかとの期待が持てます。そこで、もう少し進めます。
　3日目。2+(2x1/4)=2+2/4=10/4=2.5cm･･･(3)
　4日目。2.5+(2.5x1/5)=2.5+2.5/5=15/5=3cm･･･(4)
　5日目。3+(3x1/6)=3+3/6=21/6=3.5cm･･･(5)
　6日目。3.5+(3.5x1/7)=4+3.5/7=28/7=4cm･･･(6)

　うまく割り切れていきます。ここまできますと1/9のときも、もはや割り切れることが予測されると同時に、ある規則性までも見えてきます。
　7日目。4+(4x1/8)=4+4/8=36/8=4.5cm･･･(7)
　8日目。4.5+(4.5x1/9)=5+4.5/9=45/9=5cm･･･(8)
　・・・

　ここに至ってもはや先がわかってきました。
　「どこまで続けても割り切れるだろう」ということと、「1日ごとに0.5cmずつ高くなっていく」ということです。
　ここに「小さな数字」からやってみるという意味があるわけです。

　あとは簡単です。
　最初の高さが1cmで、毎日0.5cmずつ高くなる水位が、最初の高さの50倍、つまり50cmになるy日数を出せばいいだけです。
　それは簡単で、1+0.5y=50、y=98。したがって98日かかるということです。

　ここまできても、何かすっきりとしないものが残る方もいるかもしれません。それは「どんな数値でもいいとして、仮に高さを1cmとしたが、どんな数値でも答は98日になるのか」、さらに「設問の設定では、なぜ割り切れてしまうのか」という点です。

　それでは検証してみます。まず、最初の高さがZcmだったとすると、各式をZ倍すればいいだけではないかということになりそうですが、どうでしょうか。
　実際にやってみれば、(1)式の場合Z+Z/2=1.5Zになりますから、(2)式は1.5Z+1.5Z/3=2Zになり、だから(3)
式は2Z+2Z/4=2.5Zとなって、各式をZ倍したものになっていることが、これでわかります。

　したがって、1日ごとの差は0.5Zですから、最初の高さの50倍になる日数はｙは　Z+0.5Z*y=50Z、y=49Z/0.5Zでy=98と同じになります。（以下*印は掛け算記号） 　また、仮にプールの深さが120cmだとすると、オーナーが最初に水をはった高さは120/50=2.4cmというふうに出ます。

　では、なぜ割り切れてしまうのか。それは各式の表示を次のようにすることにより、はっきりとわかってきます。
　(1)式　1+(1x1/2)=2/2+1/2=3/2
　(2)式　3/2+(3/2x1/3)=4/2
　(3)式　4/2+(4/2x1/4)=5/2
　　　　・・・
　(n)式　(n+1)/2+{(n+1)/2*1/(n+1)}= (n+1)/2+1/2

つまり、{　}の中のアンダーラインの数値が分母と分子でちょうど打ち消すようになっているからです。
　逆に言えば、打ち消すように高さの分割を設定した問題になっているということです。
　では、プールの形が立方体という設問の但し書きは何なのか。実際、ここまでの解答を出す過程において、プールの形を考慮に入れるところがどこにもありませんでした。

　ということは、その形は円筒形であろうとひょうたん型であろうと、結果は同じになることがわかります。
　つまりその但し書きの理由は、高さだけでなく、水の量までを考慮に入れないと解けないのではと、暗に惑わせるような出題者側の仕掛けになっている、と考えられます。

　当設問の背景は、未知の数値がたくさんあるようにみえる問題でも、あるいは少数点が無限に続くような数値が脳裏にちらつく問題でも臆せず挑み、その解法糸口をいかに早く見つけ出すか、その能力の有無をみようとするものですが、さらにはｎを使っての一般解までを出してくれるような能力の持ち主の発掘を一層期待して出題されたものと思われます。

　さて、巻頭で紹介した小学校入試の問題はいかがでしたか。ひな祭り、端午の節句、入学式、七夕と、園児の誰にでも親しみのある非常にわかり易い例が対象になっていて、まさに園児向けにぴったりの問題ですが、皆さんは瞬時に解答を出したほうですか、それともあれこれと考えて結論を出したほうでしょうか。

　これは暁星小学校の入試に出された問題で、よ〜く考えると解答はいくつもあるということがわかります。仲間はずれとして、たとえば、

• 七夕（七夕は夏の行事で、他の3つは春の行事）
• 端午の節句（この日は国民の祝日で、他の3つは祝日ではない）
• 入学式（他の3つは、3月3日、5月5日、7月7日で、月と日が同じ数字）
• 七夕（他の3つは3月、4月、5月と続いているのに、七夕だけ7月と飛んで連続月となっていない）
• 七夕（他の3つは、中の2つの絵が対になっているのに対し、七夕は1つ）
• 入学式（他の3つは古い歴史があるが、入学式は近代教育が始まってから）
• ひな祭り（他の3つは、読みに濁音が入らない）

などが挙げられます。

　つまり格好の問題とした理由は、よ〜く考えると解答はいくつもあるという、いわゆる「考えるプロセス」や「考える力」を多く見ることができるという点で優れた問題だということなのです。 　あれこれ考えたという皆さんは、この考える力を自ら試されていたということになります。

　それでは設問118の解答です。

 
　では、次の問題の出題背景を考えながらやってみてください。