日常見慣れている時計を連想しながら前問に挑まれた方たちの中には、直感的な見方が先行して、つい間違ってしまったという解答もあったものと思います。特にストップォッチを片手にした面接官の前で答えるような設定の場合ならば、なおさら間違え易い問題です。
　やはり日常、あらゆることを注意深く見ていること、そしてまた深く考えを巡らしておくことが大切であることに気付かせる身近な設問でした。

　それでは、今号の設問はいかがでしょうか。

設問83 　それぞれ全員が違う会社に就職した卒業10年目の同窓生が10人集まって飲み会を開いた。ミニ同窓会での話ははずんで給料の話題になり、他の会社の同僚たちは自分と比べて給料が多いのか少ないのか、どれくらいの給料をもらっているか、各自知りたくなった。しかしその中のいくつかの会社は、各自の給料を一切公表してはならないとしており、それが会社に知れたら多額の減給処分にされることになっていた。するとその中の一人が、各自の給料を公開することなく、10人の給料の平均値は出すことができるので、それで我慢することにしようと提案した。どんな方法を提案したか。

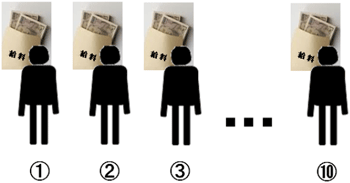
　この問題を難しくしているのは、全員の正確な給料がわからなければ、その平均値などを求めることはできないのに、そんな中でお互いの給料すらも知ることができない、という点にあります。こんな状況の中で、はたして平均値などを出すことができるのか。
　しかし、これまでの設問同様、その手がかりや糸口、突破口、あるいは偶然の思いつきなどではない解答に至る必然性が、どこかにあるはずです。

　そこでまずはこの連載を通し、これまで見てきた82個の設問のうち、似たような問題がなかったかどうかを振り返って見てみることにすると、かろうじて1問だけありました。
　もちろんまったく同じような問題ではありませんが、問いの中身が多少は似ていると思われることから、かろうじてと言ったわけです。その問題は、この連載の4問ほど前に見た設問79の錠剤の設問です。

　形も色も大きさも重さもすべて同じで、外見上まったく区別ができないＡとBの2種類の錠剤が混ざってしまった中で、両方とも同じ量だけを取り出すにはどうするか、という問題でした。どこが似ているかと申しますと、個々に混ざった状態では不明ながら、全体としての平均を求めるようにすれば解決するという問題だったからです。
　つまり、錠剤が偏った量になっている初めの状態に、新たに錠剤を加えて、AとBの量を同じにしてから平均化すれば解決する、という問題でした。

　しかし、このような解決策をこの設問83に応用することを考えた場合、新たに人を加えて全体の合計給料を平均化するなどということはできません。ところが以外にも、その解答のやり方がヒントを与えてくれるのです。
　どんなヒントか。それはこれまでにもたびたび試みてきた当連載その73でまとめた対処法とともに、一緒に考えてみるとわかってきます。

　では当設問に当てはまりそうな対処法とはどんなものかと考えてみますと、極端なケースを考えてみる、になるでしょう。そこで当設問の極端なケースとして考えられる対象となると、それは人数です。では、人数を最少の2人にした場合を考えてみます。
　この場合には、相手の給料がわからない限り、絶対に合計が出ません。これではどうしようもありません。
　しかし、もしもこのメンバーのほかに第三者がいて、2人からそれぞれの額を聞くことができれば可能ですが、そんなわかりきったことは出題する意味がありません。

　ところが、実は思いもよらないこの第三者案が、またまた大きなヒントを与えてくれることになるのです。普通、第三者という意味はメンバー外ということですが、3人目のメンバーとして、設問の設定を3人で考えてみるわけです。
　いや、たとえ3人にしたところで、その3人目もメンバーの1人なのだから、条件は同じではないか、との声が聞こえてきそうですが、実はそうでもないのです。
　なぜか。

　よ〜く考えれば、2人では不可能でも、3人となると、あることが可能になってくるということなのです。ここで発想の転換です。3人の場合、各自、本当の給料を出さなくても合計額が真の給料になる方法があるということです。
　言い換えますと、互いに自分の本当の給料とは違ったでたらめな金額を出しても、最終合計金額は本来の正確な合計金額になるという方法なのです。

　そんなバカな方法があるものかと、またまたお叱りの声が聞こえてきそうですが、そのヒントをくれるのが、先ほどの錠剤の話です。そこで見た2つの解答のうちの1つに、錠剤を半分に切ってその片方ずつを互いに集めれば、A、Bともに半分ずつ均等に分けられるという解答例がありました。
　これをそっくりそのまま設問83に応用するわけにいきませんが、ただ各個人の給料を2つに分けて使うというヒントを与えてくれるということです。

　つまり、メンバーがA、B、Cの3人とした場合、各自、自分の給料を適当に2つに分け、その2つの金額を他の2人に耳打ちするわけです。すなわち、Aが2つに分けたうちの1つをBに、もう1つをCに耳打ちするわけです。
　このとき聞き手のBとCにとって伝わってくる金額は、Aの本当の給料そのものとは違った、まさにでたらめな金額でしかありませんが、Aにとっては重要な意味をもっている金額なわけです。

　BもCも同様に自分の給料を適当に2つに分けて両隣の人に耳打ちします。そして最終的に3人が聞いた金額を合計すれば、結果、それが3人の給料の真の合計金額になっていることがわかると思います。こうしてその結果を人数の3で割れば、その平均値が簡単に出せるということです。
　この方法ならば、たとえ人数が10人になっても同様のやり方で、自分の給料を適当に分割したそれぞれの金額を両隣の人に耳打ちし、そこで全員が伝え聞いた金額の合計を10で割れば、平均値が出ます。
　したがって、この過程で各個人の給料が特定されることなく、10人全員の給料の平均値を算出できるということです。

　さて、この時点でハッピー、ハッピーで終わろうとすると、思わぬ落とし穴が待っています。ここで安心して手を休めてはダメなのです。さらにもう一歩踏み込み、ビル・ゲイツが強調している「よ〜く考えよ」を実践することにより、他にも方法があることがわかってくるのです。それを見落としてはならないということです。

　このように、でたらめな金額を有効に使えるということがわかったことから、各人の伝え方を変えれば、もう1つの方法があることがわかってくると思います。
　つまり、いくらでたらめな金額でも、それを伝える本人はそのことを知っているわけですから、その数値をその本人が後から訂正できるような方法をとればいいということです。前述の伝え方を並列方式と見なせば、ここで考えられる伝え方は直列方式です。

　つまり、最初にAがでたらめの金額をBに伝え、Bはその金額にB自身の給料を加えてCに伝える。次にCはBから聞いたその金額にC自身の給料を加えてAに戻す。そこでAはCから聞いた金額に自分の給料を加え、そこから最初にBへ伝えたでたらめな金額を引けば、結果、その金額は3人の給料の合計金額になっていることがわかると思います。それを3で割れば平均値です。
　人数が10人になっても、同様な方法で簡単に平均値が求められます。

　さて、皆さんの中には並列方式ではなく、逆にこの直列方式での解答された方もおられたかもしれませんが、同時に両方の解答をされた方はおそらく少なかったのではないでしょうか。
　しかし、問題の出題側の意向としては、同時解答者を望んでいることはおわかりいただけるものと思います。応募者が何事も常に注意深く取り組む姿勢の持ち主かどうか、こんなところではっきりと読み取れるからです。

　この設問の背景は、相手に伝える金額の中身が本当の給料の額ではなくても、全体を通して見れば、合計金額になるという方法があることに、いかに早く気付くか、そしてたとえ1つ方法がわかっても、それで安心しないでもっと注意深く掘り下げる資質の持ち主であるかどうかを見ようとするものです。

　それでは設問83の解答です。

　では、その出題背景を考えながら、次の設問を考えてみてください。