2国間の為替の差を利用して、ビールを何回でもタダで飲めるという前問はいかがでしたか。
　最初に設問を見たとき、どこか落とし穴でもあるのではと思われた皆さんも多かったかもしれませんが、どこにもそんなトリックはなく、経済活動のやり方次第ではそれが可能であるという、一面、経済学分野の問題でもありました。
　先端企業の面接試験問題は、いつも論理思考の有無を見る問題ばかりとは限りませんので、日常、常にいろんなことに目を光らせ、どん欲に知識を吸収していく姿勢が大切であることがわかると思います。

　さて、今号の設問はどうでしょうか。
 

　これはグーグル社の面接で出された問題です。回答者は3つのグループに分かれたそうです。
　Aは、ほとんど手がつかなかったグループ。Bはすぐにその解き方がわかり計算に取り掛かったものの、答までは出せなかったグループ。Cは多少の時間がかかったものの、要求されている答をしっかりと出せたグループ。

　もちろんこの中で、AとBは不合格でした。ではちゃんと計算までわかっているBと、時間はかかっても答を出したCとの違いはどこにあるのか。
　実は、その違いを見たいというのが、出題側の意図している1つなのです。以下、順次説明していく中で、それがわかってきます。

　Aグループは、他の確率問題ならおそらくその糸口をみつけて計算にとりかかるところを、この問題ではその計算に必要な分母や分子が何になるのか、はっきりと分からなかった人たちではなかったかと思われます。
　それでは計算だけはすぐにわかったというBグループの考え方に入ります。

　その考え方とは、視点を変えて見たということです。つまり30分間に自動車が存在する確率が0.95ということは、視点を変えれば、それを構成する3回の10分間のすべてに自動車が存在しなかった確率が0.05と考えたということです。
　設問に、わざわざ断り書きとして「確率は一定であると仮定します」とあることから、どの10分間も同じと考えることができるわけです。

　したがって、10分間に自動車が存在しない確率をｘとしますと、その30分間に車が存在しない確率とは、それを3回掛ければよく、ｘの3乗です。
　これと、前に視点を変えてみた0.05とを一緒にして数式にすれば、ｘ³＝0.05となり、ｘ＝0.05の立方根と出ます。
　だから、10分間に自動車が存在する確率は1−（0.05の立方根）となります。

　もちろんこれと同じになりますが、10分間で自動車が存在する確率をyとして、直接yを計算する方法もあります。
　その場合、10分間で自動車が存在しない確率は1?yとなり、30分間で自動車が存在しない確率は、それを3回掛けて(1?y)³ですから、表題にしたがって(1?y)³＝1?0.95＝0.05という式になり、y＝1?（0.05の立方根）と、同じ確率が出ます。

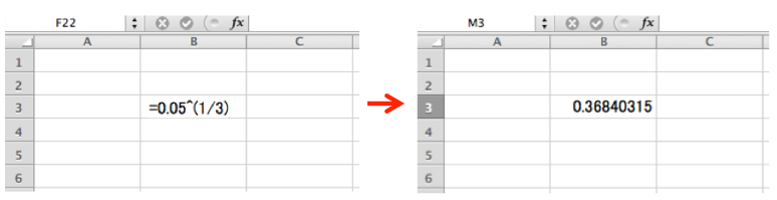
さて、ここからがBとCの違いです。0.05の立方根の数値をどうやって出すか。Bグループはここから先に進めなかったわけです。
　設問は10分間での確率はどれぐらいか、と聞いているわけですから、1?（0.05の立方根）というだけでは答の体をなしていないのです。数値まで出さなければなりません。

　パソコンがあってExcelを使えるなら、0.05の立方根の数値を求める式として＝0.05^(1/3)と入力すれば、その答0.36840315が一発で出てきますが、面接の場ですから、パソコンはもちろん電卓すらも使えないでしょう。
　しかし電卓がなくても、この設問は筆算でできるということなのです。

　設問で求められているのは「確率はどれぐらいになりますか」と「ぐらい」という表現を使っています。

　この表現で、出題側もきっちりとした数値が出ないことがわかっている上でのことだということがわかります。
　そこでxx%くらいまで出せばいいと考え、解となる1−（0.05の立方根）、つまり（0.05の立方根）を少数点以下2桁まで出せばよしとします。

　そこでこの0.05をわかりやすくするために、少し工夫をします。1000の立方根は10なので、0.05を50/1000と置き換えれば、最終的に50の立方根を10で割った数値が少数点以下2桁になればいいわけです。
　ということは、50の立方根自身は少数点以下1桁まで求めればいいことになります。

　ここまでくれば、もう90%は解けたも同然でしょう。あとは検討をつけてその少数点以下1桁の数値を追求していけばいいのです。
　ではその検討です。50の立方根がどれくらいなのかを検討をつけるために、それがどの程度の範囲にあるのか、簡単にわかるような具体的な数値を考えます。
　すると、3³＜50＜4³であることがわかります。したがって、50の立方根は3と4の間にあることから、この3から4までの間で少数点以下1桁の3.xを求めればよいわけです。
　あとは簡単な計算です。具体的な数値を入れて、この3³＜50＜4³の両サイドをせばめていけばいいだけです。

　試しに3と4の中間である3.5 の3乗、つまり3.5 x 3.5 x 3.5を筆算ですれば、42.875です。50より少ないので、今度は3.7の3乗をやってみます。これは50.653とほんの少しオーバーです。

　今度は3.6の3乗を計算しますと、46.656と出ます。そこで3.6と3.7のうち、その3乗が50に近いほうの3.7を採用すればいいことになります。
　したがって（0.05の立方根）を3.7/10として、前述の解となるyの式を使えば、y＝1?（0.05の立方根）＝1?3.7/10 ＝0.63となり、どれぐらいになるかという設問の答としては、おおよそ63%ということになるわけです。

　これで、BとCの違いや、筆算でも簡単にできることがわかったと思います。
　当設問の背景は、確率というものをよく理解しているかどうかはもちろんですが、設問をよく読み、その表現の細かなところまでに注意を払って見ているかどうか、さらには通常ならパソコンや電卓を使いたくなるような計算でも、簡単に筆算で解く道があるという、そこまで考えが及ぶ資質の持ち主かどうかを見ようとしているものです。

　それでは設問115の解答です。

 
　では、次の問題の出題背景を考えながらやってみてください。